A common measurement problem#
The picture below shows a schematic of a double crystal monochromator (DCM) like the one at NSLS-II’s BMM (Beamline for Materials Measurement) and many other beamlines. The broadband radiation from the 3-pole wiggler source is incident upon the first crystal of the DCM. At BMM, we most often use a Si(111) DCM and have the option to use Si(311) crystals. This discussion applies equally well to either crystal type (and to any other crystal monochrmoator, as well).
Monochromation of the X-ray beam happens by Bragg diffraction. The crystal is on a high-resolution rotation stage. The angle between the incident beam and the lattice planes of the first crystal is chosen so that the desired wavelength \(\lambda\) meets the Bragg condition, \(\lambda = 2d\sin(\Theta)\)
\(d\) is the spacing between the lattice planes of the crystal
\(\Theta\) is the angle between the incident beam and the lattice planes of the first crystal
By changing the angle, we change the wavelength of the beam diffracting from the first crystal. Because there is a simple relationship between wavelength and energy, we select X-ray energy for the experiment by changing the angle of the first crystal.
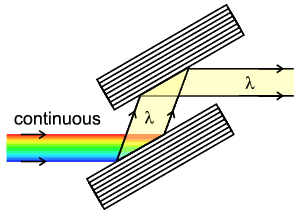
Fig. 1 Schematic of a double crystal monochromator like the one in use at BMM. (image source)#
The second crystal of the DCM is used to direct the beam downstream, towards the experimental hutch. The second crystal must at the same angle as the first crystal in order to meet the Bragg condition for the wavelength selected by the first crystal. In order to pass the X-rays with high efficiency through the DCM, the lattice planes of the first and second crystals must be parallel with accuracy within microradians.
Whenever we make a large change in energy – for example, when moving between elements with absorption edge energies that are very far apart – the parallelism of the crystals may not be maintained. So, it is prudent to minimize this difference in angle after making that large energy change. This is done by making a scan of the pitch of the second crystal, monitoring the intensity of the X-ray beam in the experimental hutch. When the second crystal is perfectly parallel to the first crystal, the intensity of the X-rays passing the the monochromator is maximized. Thus this pitch scan of the second crystal will produce a peaked lineshape. We want to place the second crystal pitch at the maximum of this peak.
At an XAFS beamline, a scan that performs this alignment is often called a “rocking curve scan” because we rock the pitch of the DCM second crystal through the parallel position, mapping out the full bandpass of the second crystal.
This rocking curve scan is a good job for Bluesky’s rel_scan().
The pitch position of the second crystal is likely to be with a short distance of the correct position, even after a large energy change. So something like this would work at the :
RE(rel_scan([quadem], dcm_pitch, -0.1, 0.1, 101))
This tells bsui to make the scan in a range of \(\pm\)100 microradians of the current position and to do so over 101 steps. That works out to steps of 2 microradians.
There is nothing horribly wrong with that … except:
It requires that the user knows that the relevant detector is on a signal chain called
quadem, which is the name of the Ophyd interface to the QuadEM electrometer interface used at BMM (note that there is not much information at the other end of that link).It requires that the user know that the name of the DCM pitch motor is
dcm_pitch.It requires that the user knows the correct scale of motion and size of step to ask for in the scan.
It will not make a plot of the data. A plotting subscription can certainly be set up, but that’s yet another thing the user must be trained to do.
It only makes the scan, it does not move to the correct position.
While it is certainly true that the user can be trained to do this operation correctly, much better would be to hide the implementation details behind a plan tailored to this specific chore. This will be discussed in the next section.